
Spacetime & FTL
Appendix I from To Sleep in a Sea of Stars
Excerpt from the Entropic Principia (revised)
. . . necessary to outline a brief overview of the fundamentals. Let this serve as a primer and quick reference guide for later, more serious studies.
FTL travel is the defining technology of our modern era. Without it, expansion beyond the Solar System would be impossible, barring centuries-long trips on generational ships or automated seed ships that would grow colonists in situ upon arrival. Even the most powerful fusion drives lack the delta-v to jet between the stars as we do now.
Although long theorized, superluminal travel did not become a practical reality until Ilya Markov codified the unified field theory (UFT) in 2107. Empirical confirmation followed soon afterward, and the first working prototype of an FTL drive was constructed in 2114.
Markov’s brilliance was in recognizing the fluidic nature of spacetime and demonstrating the existence of the different luminal realms, as outlined in the earlier, purely theoretical work of Froning, Meholic, and Gauthier around the turn of the twenty-first century. Prior to that, thinking was constrained by the limitations of general relativity.
Per Einstein’s formulations for special relativity (coupled with Lorentz trans- formations), no particle with real mass can accelerate to the speed of light. Not only would that require an infinite amount of energy, doing so would break causality, and as later, practical demonstrations have shown, the universe does not break causality on a non-quantum scale.
However, nothing in special relativity prevents a massless particle from always traveling the speed of light (i.e., a photon), nor from always traveling faster than light (i.e., a tachyon). And that is exactly what the math shows. By combining several of the equations of special relativity, the underlying relativistic symmetry between subluminal, luminal, and superluminal particles becomes clear. With regard to the superluminal, substituting relativistic mass for proper mass allows superluminal mass and energy to become definable, non-imaginary properties.
This provides us with our current model of physical space (fig. 1):
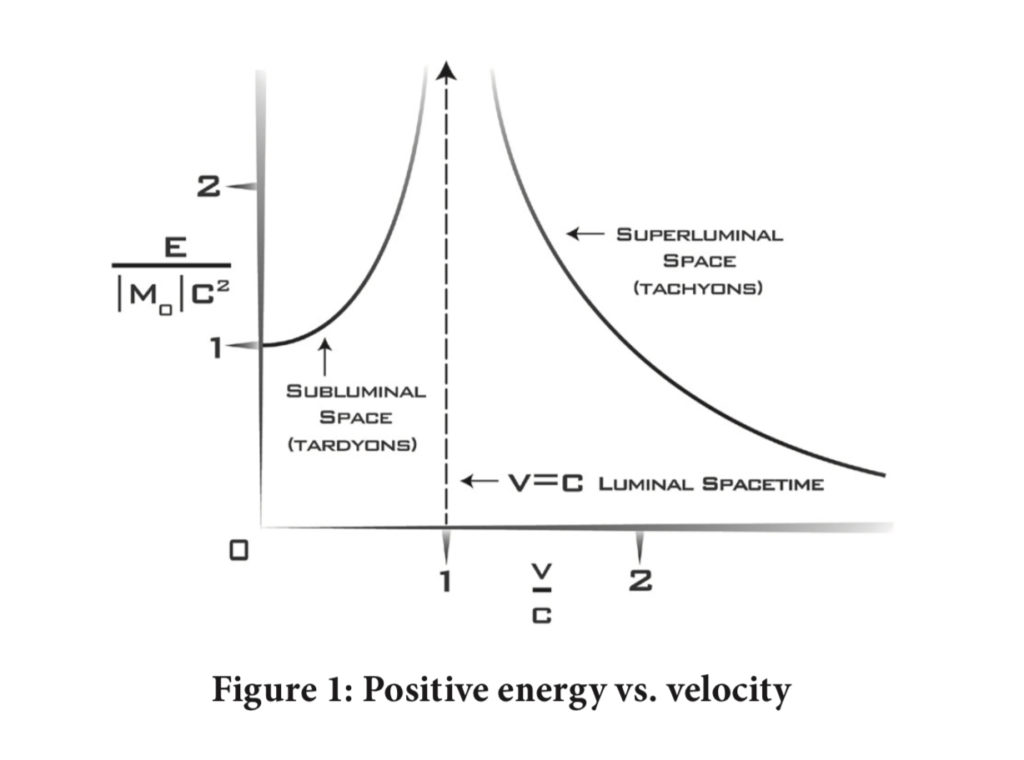
Here the v=c asymptote vertical represents the fluidic spacetime membrane (which has a negligible but non-zero thickness).
By examining this graph, a number of things will become immediately and intuitively clear. First, that just as a subluminal particle can never reach the speed of light c, neither can a superluminal particle. In normal, STL space, expending energy (e.g., shooting propellent out the back of your spaceship) can move you closer to the speed of light. So too in FTL space. However, in FTL space, the speed of light is the slowest possible speed, not the fastest, and you can never quite slow down to it, not as long as you possess mass.
Since increasing speed moves you away from c in FTL, there is no upper limit to tachyonic speeds, although there are practical limits, given the minimal level of energy needed to maintain particle integrity (remember, less energy = more speed in superluminal space). And while rest mass in subluminal space is real, positive, and increases due to special relativity as v approaches c; in luminal space, rest mass is zero and v always = c; and in superluminal space, rest mass is imaginary at v=c, but becomes real, positive, and decreases when moving faster than c.
An implication of this is the reversal of time dilation effects with regard to acceleration. In both STL and FTL, as one approaches c, one ages slower with regard to the larger universe. That is, the universe will age far faster than a spaceship barreling along at 99% of c. However, in FTL, approaching c means slowing down. If, instead, one speeds up, traveling at ever higher multiples of c, you would age faster and faster compared to the rest of the universe. This, of course, would be a major disadvantage of FTL travel if ships weren’t encased in a Markov Bubble when superluminal (more on this later).
As one can see in the graph, it is possible to have a velocity of 0 in subluminal space. What does this mean when motion is relative? That you are at rest with regard to whatever reference point you choose, whether that be an outside observer or the destination you wish to travel to. A velocity of 0 in subluminal space translates to around 1.7c in superluminal space. Fast, but still slower than the velocities of many FTL particles. Indeed, even low-end Markov Drives are capable of 51.1c. Nevertheless, if you need to reach a destination as quickly as possible, it can be worth the delta-v to bring your spaceship to a complete stop with regard to your destination before transitioning to FTL in order to get that extra 1.7c of velocity.
Were it possible to directly convert subluminal mass into superluminal mass, without a Markov Bubble, 1.7c would be the highest possible speed achievable, as there is no practical way to further accelerate the mass (i.e. further reduce the energy state of said mass) aside from chilling it. One can’t suck propellant into your tanks, for example. This would be the second major disadvantage of FTL travel, again, if not for the use of a Markov Bubble.
The third disadvantage would be the fact that matter in superluminal space behaves radically differently than in subluminal space, to the point where life as we know it would be impossible to sustain. This, again, is circumvented via a Markov Bubble.
The three different continua—the subluminal, the luminal, and superluminal— coexist within the same time and space, overlapping at every point in the universe. The luminal exists in a fluidic membrane that separates the subluminal from the superluminal, acting as an interference medium between them. The membrane is semi-permeable, and has a definite surface on both sides, upon which all EM forces exist.
The membrane itself, and thus the entirety of three-dimensional space, is made up of Transluminal Energy Quanta (TEQs), which are, quite simply, the most fundamental building block of reality. A quantized entity, TEQs possess Planck length of 1, Planck energy of 1, and a mass of 0. Their movements and interactions give rise to every other particle and field.
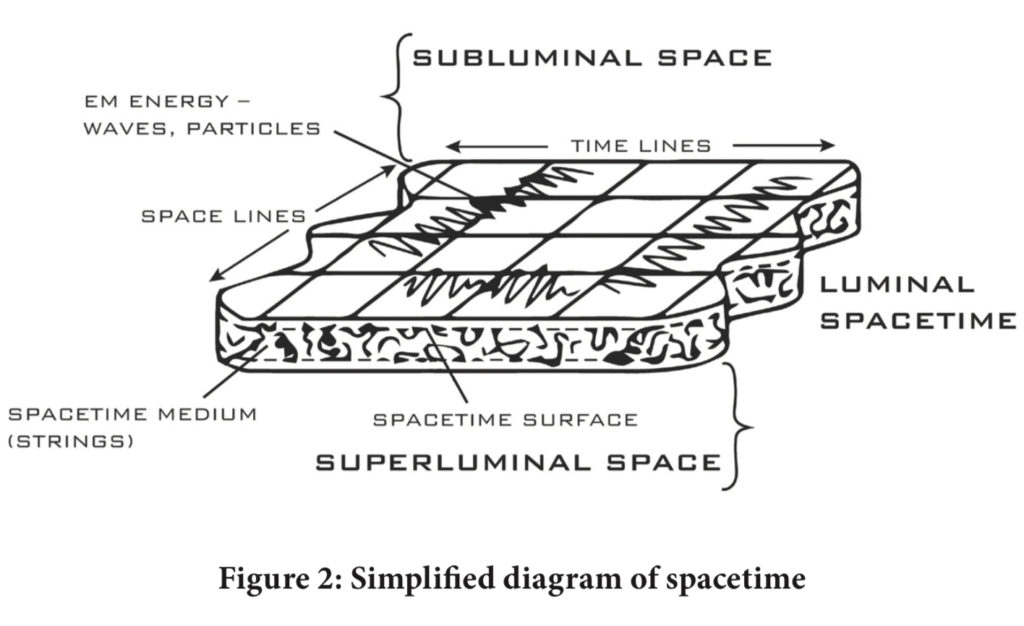
Taken as a whole, TEQs—and spacetime itself—behave in a quasi-fluidic way. Like a fluid, the luminal membrane exhibits:
• Pressure
• Density and compressibility
• Viscoelasticity
• Surface and surface tension
We will examine each of these in detail later, but for now, it’s worth noting that viscoelasticity is the property that gives rise to gravity and inertia and is what allows for all relative motion. As mass accumulates, it begins to displace the spacetime membrane, which thins beneath the object. This is gravity. Likewise, the membrane resists change, which means it takes time to displace when force is applied. (The viscousness of spacetime results in friction between boundary layers, which is the reason for the Lense–Thirring effect, aka: frame-dragging).
Since subluminal and superluminal space are physically separated by the spacetime membrane, STL mass and FTL mass can occupy the same coordinate points simultaneously, although this arrangement would be short-lived as (a) all matter in superluminal space moves at some speed faster than c, and (b) the shared membrane means that the spacetime displacement from mass, which is to say gravity, has an equal and opposite effect on the opposing realm.
An example to illustrate: in STL space, a planet will press down upon the fabric of spacetime to create the sort of gravity well we are all familiar with. At the same time, that depression will manifest in FTL space as a gravity “hill”—an equal and opposite prominence in the spacetime fabric. And the reverse is also true.
This has a number of consequences. First of which is that mass in one realm of space has a repulsive effect in the other. Stars, planets, and other STL gravitational bodies no longer act as attractors when one transitions to FTL. Quite the opposite.
The same is true of mass in superluminal space. However, since FTL contains a lower net energy density (a natural side effect of tachyons possessing a base speed of>c), and given the radically different laws and particles that exist in FTL, what happens is that the gravity hills produced by the denser, subluminal matter scatter the tachyonic mass, forcing it out and away. As confirmed by Oelert (2122), the majority of our local superluminal matter exists in a vast halo surrounding the Milky Way. This halo provides positive pressure on the Milky Way, which helps keep the galaxy from flying apart.
The gravitational effects of superluminal mass on our own subluminal realm were long a mystery. Early attempts to explain them resulted in the now- obsolete theories of “dark matter” and “dark energy.” These days, we know that the concentrations of superluminal mass between the galaxies are responsible for the ongoing expansion of the universe, and that they also affect the shape and movement of the galaxies themselves.
Whether or not tachyonic matter coalesces into the superluminal equivalent of stars and planets remains an open question. The math says yes, but so far, observational confirmation has proven elusive. The rim of the galaxy is too far away for even the fastest drones to reach, and our current generation of FTL sensors aren’t sensitive enough to pick out individual gravitational bodies at that distance. No doubt that will change in time and we will eventually be able to learn far more about the nature of superluminal matter.
Another consequence of the well/hill caused by mass-induced spacetime displacement is the effect commonly known as the Markov Limit. Before that can be explained, it will be helpful to conduct a quick review of how FTL travel and communication actually work.
In order to have unlabored transition from subluminal to superluminal space, it is necessary to directly manipulate the underlying spacetime membrane. This is done via a specially conditioned EM field that couples with the membrane (or rather, with the constituent TEQs).
In gauge theory, ordinary EM fields can be described as abelian. That is, the nature of the field differs from whatever generates it. This is true not only of EM radiation but also electron/proton attraction, and also repulsion within atoms and molecules. Nonabelian fields would be those such as the strong and weak nuclear forces. They are structurally more complicated and, as a result, display higher levels of internal symmetry.
The other, more relevant, nonabelian fields are those associated with the surface tension, viscoelasticity, and internal coherence of the spacetime membrane. These arise from the internal motions and interactions of the TEQs, the details of which far exceed the scope of this section.
In any case, it has proven possible to convert ordinary EM radiation from abelian to nonabelian by modulating the polarization of the wave energy emitted from antennas or apertures, or by tuning the frequencies of alternating current to the toroidal geometries through which the currents are driven (this is the method used by a Markov Drive). Doing so results in EM radiation with an underlying field of SU(2) symmetry and nonabelian form, as described in Maxwell’s expanded equations. This couples in an orthogonal direction with the spacetime fields via a shared quantity: the “A vector potential.” (Orthogonal, as tardyons and tachyons exhibit opposite motion directions along their packet lengths, and the conditioned EM field is interacting with both the subluminal and superluminal surfaces of spacetime.) This has often been described as traveling in a straight line along a right angle.
Once the EM field is coupled with the spacetime fabric, it becomes possible to manipulate the density of the medium. By injecting an appropriate amount of energy, spacetime itself can be made increasingly thin and permeable. So much so that at a certain point the energy density of subluminal space causes the affected area to pop into superluminal space, like a high-pressure bubble expanding/rising into an area of lower pressure.
As long as the conditioned EM field is maintained, the encompassed subluminal space can be kept suspended within superluminal space.
From the point of view of an STL observer, everything within the bubble has vanished and can only be detected by its gravitational “hill” from the other side of the spacetime membrane.
From inside the bubble, an observer will see themselves surrounded by a perfect, spherical mirror where the surface of the bubble interfaces with the outer FTL space.
From the point of view of an FTL observer, a perfectly spherical, perfectly reflective bubble will have just popped into existence in superluminal space.
Mass and momentum remain conserved throughout. Your original heading will be the same in FTL as in STL, and your original speed will be converted to the superluminal energy-equivalent.
Once the EM field is discontinued, the bubble will vanish, and everything inside will drop back into subluminal space (a process no doubt familiar to many of you). Often this is accompanied by a bright flash and a burst of thermal energy as the light and heat that built up inside the bubble during the trip are released.
A few points on the specific features of Markov Bubbles are worth mentioning:
- Since the surface of the bubble acts as a perfect mirror, it is nearly impossible to shed waste heat from a spaceship during an FTL flight. This is why it becomes necessary to put crews and passengers into cryo prior to the trip.
- Given that, it is impractical to run a fusion drive while in FTL. Thus, Markov Drives—which require a not-inconsiderable amount of power to generate and maintain a conditioned EM field of sufficient strength— rely upon stored antimatter to produce said power. This is more efficient and results in the least amount of waste heat.
- Although a Markov Drive and the spaceship around it contain a large amount of compressed energy by FTL standards, the only energy that superluminal space sees is that which appears via the surface of the bubble. Thus, the more efficient a Markov Drive (i.e., the less energy it uses to generate the conditioned EM field) the faster you can travel.
- Were one unfortunate enough to collide with a chunk of FTL mass, this would result in immediate disruption of the Markov Bubble and immediate return to STL space, with possible catastrophic consequences, depending on one’s location.
- The less energy you use to generate a Markov Bubble, the increasingly delicate the bubble becomes. Large gravitational hills, such as those around stars and planets, are more than strong enough to disrupt the bubble and dump you back into normal, subluminal space. This is what is known as the Markov Limit. With adequate computational powers, the limit can be lowered, but it cannot be removed entirely. Currently, Markov Drives cannot be activated in a gravitational field stronger than 1/100,000 g. This is why, in Sol, spaceships have to fly out to a distance equivalent to the radius of Jupiter’s orbit before they are able to go FTL (although if you’re actually near Jupiter, you’ll have to fly out even farther still).
As annoying as the Markov Limit is—no one likes having to sit through several more days of travel after weeks or months in cryo—it has actually proven to be a good thing. Because of it, no one can drop an FTL asteroid directly onto a city, or worse. Were there no Markov Limit, every spaceship would be far more of a potential threat than they already are and defense against surprise attacks would be basically impossible.
We are also fortunate that the viscoelasticity of spacetime precludes superpositional bombs. If a ship in FTL space flies over a mass in STL space that produces less than 1/100,000 g, and the ship returns to subluminal space at that precise moment, the ship and the mass will push each other apart with equal force, preventing either object from intersecting. If they did intersect, the resulting explosion would be on par with an antimatter detonation.
Once a spaceship has entered superluminal space, straight-line flight is usually the most practical choice. However, a limited amount of maneuverability is possible by carefully increasing the energy density on one side or another of the bubble. This will cause that side of the spaceship to slow, and thus the vessel as a whole to turn. But it is a gradual process and only suitable for small course corrections over long distances. Otherwise you risk destabilizing the bubble. For more substantial changes, it is better to drop back into subluminal space, reorient, and try again.
Any changes in heading that occur in FTL will be reflected upon returning to STL. Likewise any changes to total momentum/speed, with the degree of change being inversely proportional.
Technically it is possible for two ships in FTL to dock, but the practical difficulties of matching exact velocities, as well as the mathematics of merging Markov Bubbles, means that while it has been done with drones, no one—to our knowledge—has been crazy enough to try it with crewed ships.
Although a ship within a Markov Bubble can never directly observe its FTL surroundings, some level of sensory information is possible. By pulsing the bubble at the appropriate frequencies, FTL particles can be created on the outer surface of the membrane, and these can be used both as a form of radar as well as a signaling mechanism. With careful measurement, we can detect the return of the particles when they impinge upon the bubble, and this allows us to interact with superluminal space, albeit in a crude manner.
This is the same method by which FTL comms and sensors work. Both may be used far closer to a star or planet than one can maintain a Markov Bubble, but as with the bubble, there is a point at which the associated gravity hills become too steep for all but the slowest, most energetic FTL signals to climb.
Due to the protection of the bubble, a ship retains the inertial frame of reference it had prior to FTL, which means it does not experience the extreme time dilation that an exposed superluminal particle would. Nor does it experience any relativistic effects at all (the twins of the famous twin paradox will age at the same rate if one of them takes an FTL flight from Sol to Alpha Centauri and back).
This, of course, leads us to the question of causality.
Why, one might ask, doesn’t FTL travel allow for time travel, as all the equations for special relativity seem to indicate? The answer is that it doesn’t, and we know this because . . . it doesn’t.
Although that may seem facetious, the truth is that the debate remained unsettled until Robinson and the crew of the Daedalus made the first FTL flights. It took empirical experimentation to answer the question of time travel for certain, and it was only after the fact that the supporting math and physics were fully developed.
What was found was this: no matter how fast a superluminal voyage—no matter how many multiples of c your spaceship travels—you will never be able to return to your origin point before you left. Nor for that matter can you use FTL signals to send information into the past. Some amount of time will always elapse between departure and return.
How is this possible? If one is at all familiar with light cones and Lorentz transformations, it should be blindingly obvious that exceeding the speed of light results in being able to visit the past and kill your own grandfather (or something equally absurd).
Yet we cannot.
The key to understanding this lies in the fact that all three luminal realms belong to the same universe. Despite their seeming separation (as it appears from our normal, subluminal point of view), the three are part of a larger, cohesive whole. And while local violations of physical laws may appear to occur in certain circumstances, on a global scale, those laws are upheld. Conservation of energy and momentum, for example, are always maintained across the three luminal realms.
Adding to that, there is a certain amount of crossover. Gravitational distortions on one side of the luminal barrier will have a mirrored effect on the other. Thus, an object moving in subluminal space will leave an STL gravitational distortion in the equivalent FTL space. Waves from the distortion will propagate outward at c no matter what, but the movement of the gravitational center will be less than c. And the reverse is true for a superluminal gravitational mass, which would leave an FTL track of spacetime ripples through normal, subluminal space. (Of course, no such FTL tracks were detected prior to the invention of the Markov Drive, but that was a result of—in most cases—their extreme weakness and the distance of most superluminal matter from the main body of the Milky Way.)
Note: it’s important to remember that just as anything moving faster than c in subluminal space could theoretically be used to arrange a causality violation, so too could anything moving slower than c in superluminal space. In FTL, c is the minimum speed of information. Above that, relativity and non-simultaneity are maintained, no matter how fast you might be going.
Even without the existence of a Markov Drive, we now have a situation where natural phenomena seem to be violating the light-speed barrier on both sides of the spacetime membrane, but again, without inducing any causality violations.
The question returns: Why is that?
The answer is twofold.
One: no particle of real mass ever breaks the light-speed barrier in either the sub- or superluminal realm. If one did, we would see all of the paradoxes and causality violations predicted by traditional physics.
Two: just as TEQs form the basis for every subluminal particle, they also form the basis for every superluminal particle. As their name implies, TEQs are capable of existing in all three realms at once, and they are capable of mov- ing as slow as the slowest STL particle and as fast as the fastest FTL particle— which is very fast indeed, limited only by the lower boundary of energy needed to maintain particle coherence, and even then, TEQs can move faster still given their Planck energy of 1.
Thus, with the discovery of TEQs, we have an object that is capable of conveying information far faster than the speed of light. Normally this only occurs in the superluminal realm, but any TEQ is capable of such speeds, and they often transfer from sub- to superluminal velocities as their position within the spacetime membrane changes. These changes are responsible for much of the quantum weirdness seen at small scales.
The light cone, as it were, of an observer using TEQs for informational gathering would be far, far wider than if they were only using photons (wider, but not complete; TEQs have a finite velocity). The wider light cone—or TEQ cone—expands the total set of events that can be regarded as simultaneous. Although non-simultaneity and relativity are maintained throughout all three luminal realms (when considered as a whole), the immense velocity of TEQs reduces the events that can be considered non-simultaneous to a far smaller number, and those that are lie outside the fastest speed of an FTL particle. And while, in theory, the universe remains fundamentally relative, in practice, the vast majority of events may be regarded as ordered and causal.
This means that when a ship goes FTL, it cannot induce any causality violations within superluminal space, as the Markov Bubble is a superluminal particle/object and behaves as such. And when a ship drops back to STL, no causality violations occur because travel times are always slower than the top speed of the TEQs (i.e., the speed of information).
Where a paradox would have occurred in subluminal space, events are found to have proceeded in a causal relationship, one after another, without any contradiction. From a distance, it may appear that one can send a piece of information back to its origin point before it was transmitted, but appears is the word to keep in mind. In actuality, no such thing is possible. If one tries, the return transmission will never arrive any sooner than one unit of TEQ Planck time (where TEQ Planck time is defined as the length of time for a TEQ at maximal speed to traverse one unit of Planck length).
As a result, whenever one sees the possibility for a causality violation in subluminal space, one is, in essence, seeing a mirage. And whenever one tries to exploit said possibility, one will fail.
This renders a large number of observations in our subluminal universe illusionary. Prior to the invention of the Markov Drive (or failing that, detection of FTL gravitational signals), none of this mattered. Relativity was maintained throughout because FTL travel and communications weren’t possible. Nor could we accelerate a spaceship to high enough relativistic speeds to really begin to investigate the issue. Only now, with access to both the sub- and superluminal realms, has the truth become clear.
As the light signatures of our modern-day FTL trips begin to reach the nearby stars, an observer positioned there with a powerful enough telescope would see a confusing series of images as ships and signals pop out of nowhere, seemingly out of order. However, by observing TEQs instead of photons, the true order of events may be established (or by physically traveling to the sources of the images).
The exact mechanism that prevents causality violations in STL space is the top velocity of the TEQs. As long as that isn’t broken (and no known mechanism would allow for this), FTL will never allow for time travel into the past. And for that we should be grateful. A non-causal universe would be sheer chaos.
Special Thanks and Acknowledgements
On the technical side of things: Gregory Meholic, who was kind enough to let me use his Tri-Space theory as the basis for my FTL system (as well as several of his graphs, which were redrawn for Appendix I). He also answered scores and scores of questions as I struggled to understand the specifics of how it worked. Apologies to him for bastardizing his theory in one or two places in the interests of fiction. Sorry Greg! Also Richard Gauthier—who originated the idea of TEQs—and H. David Froning Jr., who invented the technical groundwork for conditioned EM fields, which I used as the basis for my Markov Drives. And last but not least, Winchell Chung and the Atomic Rockets website (www.projectrho.com/rocket/). The best resource for anyone wanting to write realistic science fiction. Without it, the ideas in this book would have been far less interesting.
Christopher Paolini, Afterword & Acknowledgements, To Sleep in a Sea of Stars
